How to choose your experimental design
Experimental design choices
In agricultural research it is important to choose the right experimental design at the beginning of your trial so that the analyses produced at the end of the season are statistically meaningful. Before we look further at the different types of designs, it is worth taking some time to understand why we need them.
Suppose a plant breeder chooses two plots of land that are as alike as possible and sows the same variety in each plot. Even if the breeder treats each plot with identical husbandry, when she measures the yield from each plot, they will differ.
This difference is called experimental error. For the breeder to make a sound decision about the performance of two or more varieties, she must have an estimate of the experimental error in the trial. If the measured difference between varieties is greater than the experimental error, then she can be confident one variety is outperforming the other. The breeder has two tools at her disposal to measure experimental error: replication and randomization.
The breeder has two tools at her disposal to measure experimental error: replication and randomisation.
Replication helps to make more precise estimates of the experimental error, and randomisation prevents any other uncontrolled sources of variation from biasing the results.
Together, replication and randomisation define the experimental design and there are a number of common types that have been developed for agricultural researchers to use:
• Completely Randomised Design
• Randomised Complete Block
• Latin Squares
• Split Plot Design
• Strip Plot Desing
to name a few.
The most appropriate design for a particular trial will depend on the various constraints of the trial, such as: the number of varieties being tested, size of the machinery used to apply treatments, the size of the detectable differences between treatments, and the resources required (time, space and money) to operate the trial.
Completely Randomised Design
A completely randomised design is the simplest of all the designs. In a completely randomised design, each treatment is equally likely to be allocated to a plot. The completely randomised design has many advantages: any number of treatments and replications can be accomodated; the analysis is simple and can easily cope with missing plots; the degrees of freedom of the error is higher than any other design of the same number of treatments, allowing for a more accurate estimate of experimental error.
Completely randomised designs have one disadvantage in that they require the plots to be more or less completely uniform. If there is ahigh degree of variability in the plots, for example from soil variation, then the estimate of the experimental error will be less precise and true differences between treatments may not be detectable.
Typically, completely randomised designs are used when the trial site is known to be particularly uniform. They can also be very useful in scenarios where a large number of plots are expected to fail during the trial, as the analysis of the surviving plots remains simple.
Completely randomized designs are used when the trial site is known to be particularly uniform.
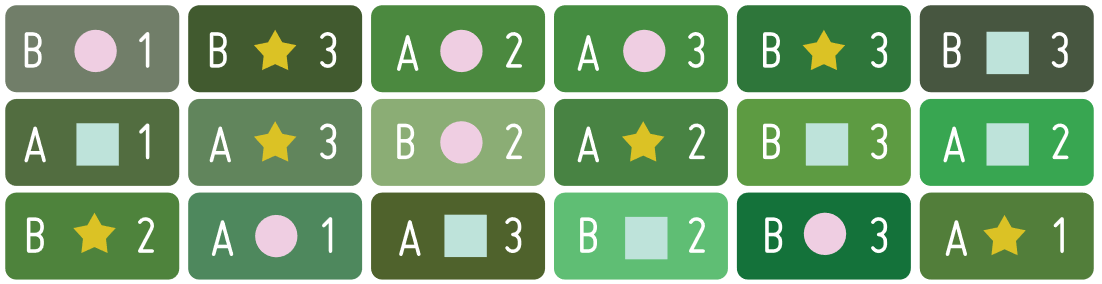

Randomised Complete Block Design
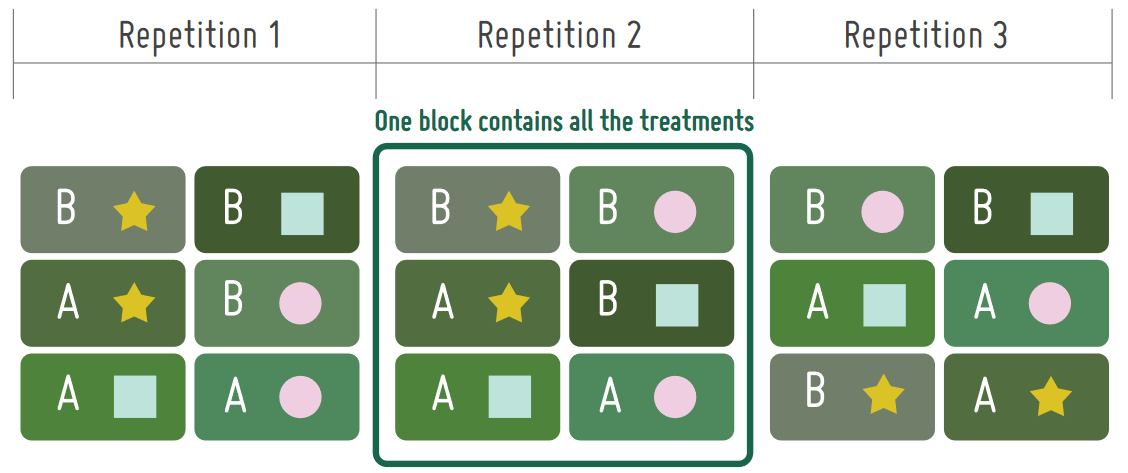
Randomised complete block design is by far the most common experimental design found among agricultural researchers today. Plots are grouped into blocks based on their similarity, e.g. similar soil types. Plots are then assigned treatments in such a way that each treatment occurs once in each block. Therefore, each block contains every possible treatment, hence the ‘complete block’ design.
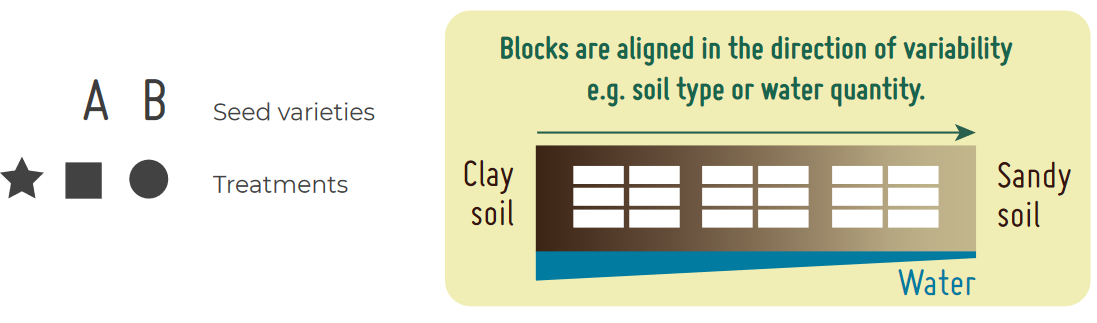
When planning a complete block design, the researcher must ensure that any variability with the block is minimized, while variation between blocks should be maximised. If there is little variability on the trial site, blocks can be placed next to each other. However, if there is a gradient of variability where the trial is to be located, blocks should be arranged in lines perpendicular to the gradient. In fact, there is no need for the blocks to be adjacent to one another apart for practical reasons of measurement and treatment activities.
Plots are grouped into blocks based on their similarity and each treatment occurs once in each block
This can be useful when a trial location straddles different soil types for example.
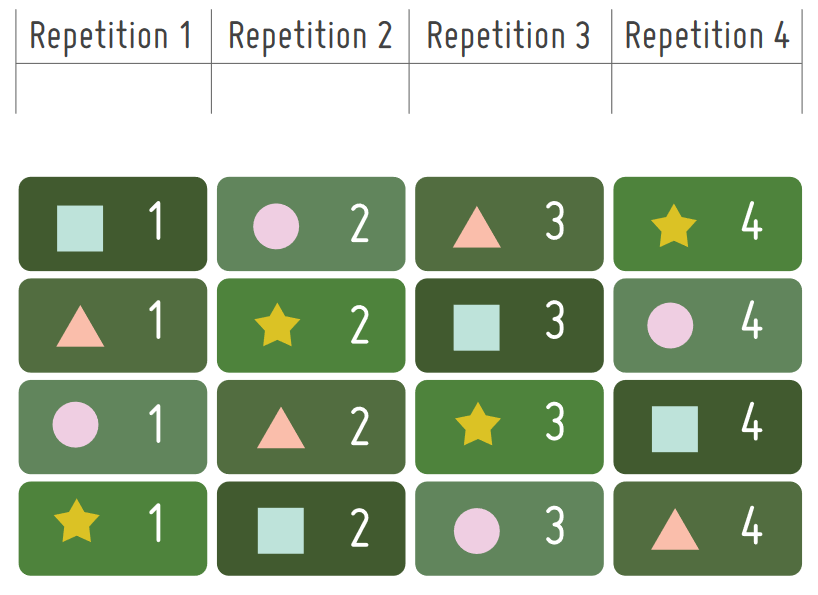
Latin Square Design
As the name suggests, this design forms a square divided up into an equal number of rows and columns. Each treatment or variety is placed so that it appears exactly once in each row and column.
The main benefit of the Latin square design is that they can account for two sources of variation in the trial site. For example, the field in which the trial is conducted may have a fertility gradient in one direction and a slope in another.
Latin square can account for two sources of variation in the trial site
Latin square designs are not frequently used in agricultural trials as they have several disadvantages to other designs. Firstly, since the number of plots is the square of the number of treatments, trials can become very large and costly to run. Secondly, any mistakes made during the trial such as misapplied treatments can make the data difficult to analyse.
Thirdly, if there are few treatments (less than 4) the degrees of freedom of the error is low, which in turn results in a larger experimental error estimate.

Split Plot Design
It is common for agricultural trials to have multiple treatment factors, for example testing three different nitrogen rates combined with three different cultivation types. This could be accomplished with a randomised complete block design where every combination of the two factors occurs in each block. However, some treatments can be difficult or impossible to apply in this fashion.
Cultivation equipment is typically at the scale of a commercial farm and requires large plots whereas nitrogen can be applied by hand to much smaller plot sizes.
To deal with these complications, the agricultural researcher has the split plot design to call upon. In this design, one factor is assigned to large plots in a randomised complete block design. These large plots are then subdivided into smaller plots, which have the treatments of the other factor applied at random.
Cultivation equipment is typically at the scale of a commercial farm and requires large plots
As described above, the main advantage of split plot designs is to allow more efficient handling of treatment factors which require different plot sizes. Split plot designs also allow for the possibility to add new treatments to an experiment in progress by simply adding more large plots to the blocks.
Since there are two plot sizes, split plot designs produce two experimental errors, one for each size. This can often mean large differences in the observations are needed to show significant difference. Split plot designs also have the disadvantage of requiring more complex analysis.
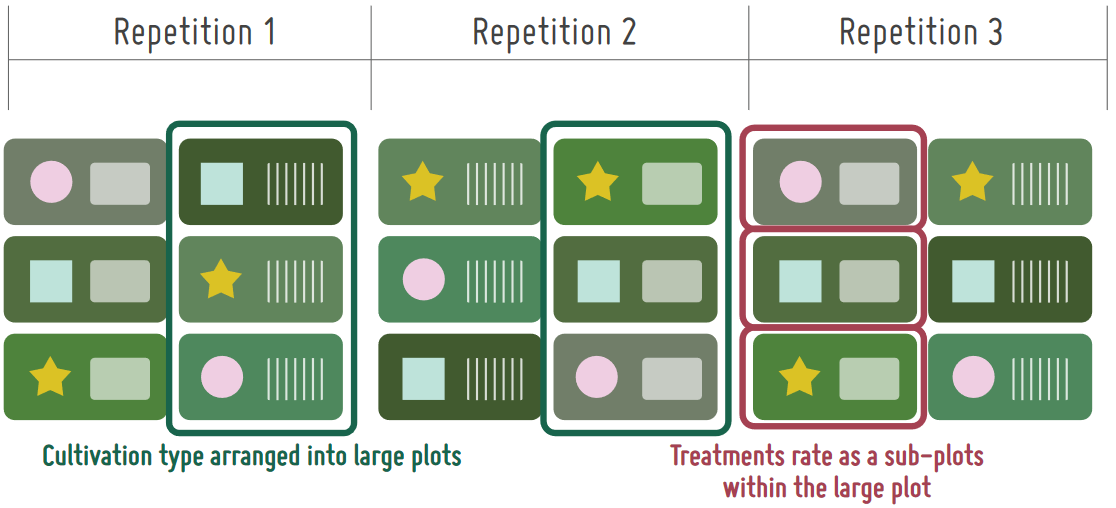
Strip Plot Design
A useful variation on the split plot design is the strip plot design. In circumstances where each treatment factor is easiest to apply in passes or strips, strip plot designs can be used. In these designs, one factor is assigned to strips running within each block, and each block has its own randomisation. The second factor is then applied in strips perpendicular to the first, again with unique randomisation for each block.
The result is like a checkerboard of treatments. Strip plot designs have similar advantages and disadvantages to split plot designs, mainly allowing efficient setup of the trial.
In these designs, one factor is assigned to strips running within each block, and each block has its own randomisation.


Incomplete Block Design
When the number of treatments grows, it can be increasingly difficult to maintain uniformity of blocks under a randomised complete block design. This is especially found in breeding trials where a large number of selections are tested. In order to maintain blocks small enough to remain uniform, only a subset of treatments can appear in any give block, hence the name ‘incomplete block’ design. There are a number of different incomplete block designs available to the researcher but it is a too complex topic to go into significant detail here. One such design that QuickTrials provides is an alpha lattice, which has some specific requirements:
• The number of plots per block (p) must be smaller than the square root of the number of treatments (t);
• The number of replicates has to be smaller or equal to the ratio p/t;
• The number of treatments has to be a multiple of p.









